파이썬 코드를 작성하며 간단히 살펴보는 선형대수
미디엄에서 파이썬 코드와 함께 선형대수를 간단히 살펴보는 좋은 글을 발견하여 수정한 결과입니다.
이후 문서를 틈틈이 개선해볼 생각입니다.
최초작성 2025. 6. 22
Vector
단위 벡터
벡터 연산
벡터 덧셈
스칼라 곱 (scalar multiplication)
내적(Dot product)
벡터 공간(Vector space)
영공간(Null space)
생성공간(Span)
기저(Basis)
일차 독립(Linear Independence)
행렬(Matrix)
함수로서의 행렬
선형 변환(Linear Transformation)
역행렬(Inverse Matrix)
특이행렬(Singular Matrix)
단위 행렬(Identity matrix)
대각 행렬(Diagonal Matrix)
직교 행렬(Orthogonal matrix)
행렬 곱셈(Matrix multiplication)
대각합(Trace)
행렬식(Determinant)
계수(Rank)
고유벡터(Eigenvectors)와 고유값(Eigenvalues)
참고
Vector
벡터는 선형 대수에서 가장 기본이 되는 개념입니다. 벡터를 이해하는 방법은 세 가지가 있습니다.
1. 물리학 - 벡터를 화살표로 나타낼 수 있습니다. 화살표는 크기(얼마나 긴지)와 방향(어느 방향을 가리키는지)을 갖습니다. 종이 위에 그리면 2차원, 우리가 사는 공간에서는 3차원이 됩니다. 예를 들면 바람의 세기와 방향, 자동차가 움직이는 속도와 방향이 있습니다.
2. 컴퓨터 - 벡터를 숫자들의 목록으로 나타냅니다. [3, 4]처럼 숫자를 순서대로 나열한 것이죠. 숫자가 2개면 2차원, 3개면 3차원입니다.
3. 수학 - 벡터는 다음 두 가지 연산이 가능한 모든 객체를 말합니다.
- 벡터 덧셈 - 두 벡터 u와 v를 더해서 새로운 벡터 u + v를 만들 수 있어야 합니다
- 스칼라 곱셈 - 벡터 v에 실수 c를 곱해서 새로운 벡터 cv를 만들 수 있어야 합니다
다음 규칙을 모두 만족해야 벡터입니다.
- u + v = v + u (덧셈의 교환법칙)
- (u + v) + w = u + (v + w) (덧셈의 결합법칙)
- 0벡터가 존재해서 v + 0 = v
- 각 벡터 v에 대해 -v가 존재해서 v + (-v) = 0
- c(u + v) = cu + cv (분배법칙)
- (c + d)v = cv + dv (분배법칙)
- c(dv) = (cd)v (스칼라 곱의 결합법칙)
- 1v = v
벡터를 화면에 그려주는 코드입니다.
벡터의 화살표 방향은 각 벡터의 방향을 나타내며, 길이는 벡터의 크기(또는 magnitude)를 나타냅니다.
단위 벡터
단위 벡터는 크기가 1인 벡터로, 크기와 관계없이 벡터의 방향을 나타낼 때 자주 사용됩니다.
벡터 연산
벡터 덧셈
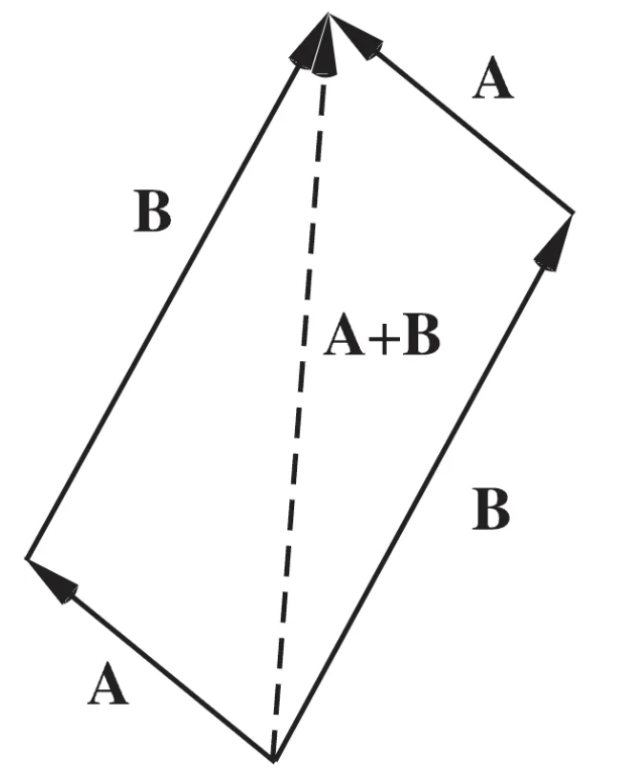
왼쪽 그림은 두 벡터 A와 B가 한 점에서 시작하여 평행사변형을 형성하고 있습니다. 점선으로 표시된 대각선이 바로 두 벡터의 합 A+B를 나타냅니다. 이는 벡터 덧셈의 평행사변형 법칙으로, 두 벡터를 인접한 변으로 하는 평행사변형을 그렸을 때 대각선이 합벡터가 됩니다.
오른쪽 그림은 두 벡터의 합 A+B를 더 간단하게 표현한 것입니다.
차원이 같은 두 개의 벡터를 더하여 새로운 벡터를 생성합니다. 대응하는 성분끼리 더해주면 됩니다.
- 2차원: (a₁, a₂) + (b₁, b₂) = (a₁+b₁, a₂+b₂)
- 3차원: (a₁, a₂, a₃) + (b₁, b₂, b₃) = (a₁+b₁, a₂+b₂, a₃+b₃)
스칼라 곱 (scalar multiplication)
스칼라 곱은 벡터에 스칼라(숫자)를 곱하여 원래 벡터와 같은 방향(스칼라가 음수인 경우 반대방향)의 벡터를 만들되, 스칼라의 절대값에 따라 벡터의 크기가 조정된 벡터를 만드는 것을 말합니다.
실행 결과입니다.
원래 빨간색 벡터에 스칼라 3을 곱한 결과 파란색 벡터의 크기는 원래 벡터의 크기의 3배가 되었습니다.
내적(Dot product)
두 벡터의 유클리드 크기와 벡터 사이의 각도 코사인의 곱으로, 벡터의 길이와 방향 관계를 모두 반영합니다.
벡터의 내적은 한 벡터가 다른 벡터에게 얼마나 많은 힘이나 에너지를 전달하는지를 측정하는 개념입니다. 이를 통해 원래 벡터가 얼마나 강화되었는지 알 수 있으며, 그 결과는 양수, 음수, 또는 0의 값을 가집니다.
구체적으로 설명하면, 두 벡터가 같은 방향을 향할 때는 서로의 힘을 보태주어 양수 결과가 나오고, 반대 방향을 향할 때는 서로 상쇄되어 음수 결과가 나옵니다. 만약 두 벡터가 수직으로 만난다면 서로에게 영향을 주지 않아 결과값이 0이 됩니다.
이는 마치 두 사람이 함께 물건을 밀 때와 같습니다. 같은 방향으로 밀면 물건이 더 잘 움직이고, 서로 반대 방향으로 밀면 힘이 상쇄되며, 각자 다른 방향으로 밀면 서로의 움직임에 영향을 주지 않는 것과 비슷한 원리입니다.
내적이 0이면 벡터가 직교임을 알 수 있습니다. cos 90은 0이기 때문입니다.
실행 결과입니다. 두 백테의 내적이 출력됩니다.
Dot Product: 8
벡터 공간(Vector space)
벡터 공간이란 벡터들의 집합인데, 이 벡터들은 두 가지 기본 연산이 가능해야 합니다. 첫째는 벡터끼리 더할 수 있어야 하고, 둘째는 벡터에 스칼라(숫자)를 곱할 수 있어야 합니다.
예를 들어 생각해보면, 2차원 평면에서 화살표들을 상상해보세요. 이 화살표들을 서로 이어 붙여서 더할 수 있고, 화살표를 2배로 늘이거나 반으로 줄일 수도 있습니다. 이런 화살표들의 모음이 바로 벡터 공간의 한 예입니다.
다만 아무 벡터 집합이나 벡터 공간이 되는 것은 아닙니다. 벡터 공간이 되려면 특정한 규칙들을 만족해야 하는데, 이를 공리라고 합니다. 이 공리들은 덧셈과 스칼라 곱셈이 우리가 기대하는 대로 자연스럽게 작동하도록 보장해주는 조건들입니다.
다음 8개의 공리를 만족하는 벡터 집합만이 벡터 공간입니다.
덧셈에 관한 공리들
1. 결합법칙 - (u + v) + w = u + (v + w) : 벡터를 더하는 순서를 바꿔도 결과가 같습니다.
2. 교환법칙 - u + v = v + u : 벡터를 더하는 순서를 바꿔도 결과가 같습니다.
3. 영벡터 존재 - 0 + v = v가 되는 영벡터 0이 존재합니다.
4. 역원 존재 - 각 벡터 v에 대해 v + (-v) = 0이 되는 -v가 존재합니다.
스칼라 곱셈에 관한 공리들
5. 결합법칙 - a(bv) = (ab)v : 스칼라를 곱하는 순서를 바꿔도 결과가 같습니다.
6. 항등원 - 1 × v = v : 1을 곱하면 벡터가 그대로 유지됩니다.
덧셈과 스칼라 곱셈 사이의 관계
7. 분배법칙 1 - a(u + v) = au + av : 스칼라 곱셈이 벡터 덧셈에 분배됩니다.
8. 분배법칙 2 - (a + b)v = av + bv : 벡터 곱셈이 스칼라 덧셈에 분배됩니다.
영공간(Null space)
영공간이란 행렬과 곱했을 때 결과가 영벡터(모든 성분이 0인 벡터)가 되는 벡터들의 집합입니다. 다시 말해, Ax = 0이라는 방정식의 해가 되는 모든 벡터 x들을 모아놓은 것이 영공간입니다.
2차원 평면에서 예를 들어보면, 여러 화살표들이 있을 때 행렬을 곱하면 대부분의 화살표는 다른 방향이나 크기로 변하지만, 영공간에 속하는 화살표들은 모두 원점으로 축소되어 사라집니다. 이런 벡터들이 모여 있는 영역이 바로 영공간입니다.
예를 들어, 어떤 행렬이 특정 방향의 모든 벡터를 0으로 만든다면, 그 방향에 있는 직선 전체가 영공간이 됩니다.
실행결과 계산된 영공간을 출력합니다.
[[-0.89442719]
[ 0.4472136 ]]
생성공간(Span)
두 개의 벡터 v와 w를 가지고 새로운 벡터를 만드는 방법은 각각의 벡터에 임의의 실수를 곱해서 더하는 것입니다. 즉, av + bw 형태로 만들 수 있는 모든 벡터들을 일차결합이라고 합니다.
그리고 이렇게 만들어낼 수 있는 모든 벡터들이 모인 집합을 생성공간(span)이라고 부릅니다. 즉, span{v, w}는 v와 w의 모든 가능한 일차결합들로 이루어진 공간입니다.
2차원 평면에서 구체적으로 보면, 대부분의 벡터 쌍 v와 w의 span은 전체 평면이 됩니다. 마치 두 개의 서로 다른 방향 화살표가 있을 때, 이 화살표들을 적절히 늘이고 줄여서 조합하면 평면상의 어떤 지점이든 갈 수 있는 것과 같습니다. 이때 도달할 수 있는 모든 지점들의 집합이 바로 span입니다.
예를 들어, 오른쪽으로 가는 벡터와 위쪽으로 가는 벡터가 있다면, 이 둘의 span은 전체 2차원 평면이 됩니다.
두 벡터가 일직선상에 있을 때는 상황이 달라집니다. 예를 들어, 한 벡터가 오른쪽으로 향하는 화살표이고 다른 벡터도 같은 오른쪽 방향(또는 반대인 왼쪽 방향)으로 향한다면, 이 두 벡터는 사실상 같은 직선 위에 있는 것입니다.
이런 경우에는 두 벡터의 일차결합으로 만들 수 있는 모든 점들이 하나의 직선으로만 제한됩니다. 아무리 계수 a와 b를 바꿔가며 av + bw를 계산해도, 결과는 항상 같은 직선 위의 점들만 나오게 됩니다.
구체적인 예로 설명하면, 벡터 v가 (2, 0)이고 벡터 w가 (4, 0)이라고 해보세요. 둘 다 x축 방향으로만 향하고 있습니다. 이 경우 av + bw = a(2, 0) + b(4, 0) = (2a + 4b, 0)이 되어, 결과는 항상 x축 위의 점들만 나옵니다. 즉, 전체 2차원 평면을 채우지 못하고 원점을 통과하는 x축이라는 하나의 직선으로만 제한되는 것입니다.
이것이 바로 두 벡터가 일직선상에 있을 때 생성공간(span)이 직선으로 축소되는 이유입니다.
다음 코드는 두 벡터의 생성공간을 시각적으로 보여주는 프로그램입니다.
이 코드를 실행하면 그래프상에 보라색 점들이 격자 모양으로 분포되어 나타납니다. 이 점들은 v1과 v2의 일차결합으로 만들 수 있는 벡터들의 끝점들을 보여줍니다.
두 벡터 v1과 v2가 서로 다른 방향을 향하고 있기 때문에, 이들의 생성공간은 전체 2차원 평면을 덮을 수 있습니다. 만약 더 많은 계수 값들을 사용한다면, 점들이 평면 전체를 빽빽하게 채우는 모습을 볼 수 있을 것입니다.
기저(Basis)
기저란 벡터 공간을 만들어내는 가장 기본적인 벡터들의 집합입니다. 이 기저 벡터들은 두 가지 중요한 특징을 가집니다.
첫째, 일차독립성: 기저 벡터들은 서로 독립적입니다. 즉, 한 벡터를 다른 벡터들의 조합으로 만들 수 없습니다. 마치 레고 블록에서 빨간 블록을 파란 블록과 노란 블록으로 아무리 조합해도 만들 수 없는 것과 같습니다.
둘째, 생성능력: 이 기저 벡터들의 일차결합으로 그 공간의 모든 벡터를 만들어낼 수 있습니다.
기저 벡터들이 있으면 벡터 공간의 모든 벡터를 만들어낼 수 있습니다.
예를 들어, 오른쪽으로 향하는 벡터 하나와 위쪽으로 향하는 벡터 하나가 있으면 평면상의 어떤 점이든 갈 수 있습니다. 이 두 벡터가 바로 2차원 평면의 기저가 됩니다.
가장 일반적인 기저는 표준 기저입니다. 다음 두 벡터는 2차원 평면의 표준 기저입니다.
- e₁ = [1, 0] (x축 방향으로 1만큼)
- e₂ = [0, 1] (y축 방향으로 1만큼)
이 두 벡터로 평면 상의 모든 점을 만들 수 있습니다. 예를 들어:
- [3, 5] = 3×[1, 0] + 5×[0, 1] = 3e₁ + 5e₂
- [-2, 4] = -2×[1, 0] + 4×[0, 1] = -2e₁ + 4e₂
다음 처럼 다른 기저를 사용할 수도 있습니다.
- v₁ = [1, 1] (오른쪽 위 대각선 방향)
- v₂ = [1, -1] (오른쪽 아래 대각선 방향)
이 두 벡터를 기저로 사용하여 앞에서 예로 들었던 점 [3, 5]을 표현하면: [3, 5] = 4×[1, 1] + (-1)×[1, -1] = 4v₁ - v₂ 가 되어 앞에서 한 것과 표현이 다르게 됩니다. 기저가 바뀌면 똑같은 점이라도 표현이 달라집니다.
기저가 아닌 경우를 예로 들어봅니다.
이 경우 u₂ = 2×u₁이므로 일차독립이 아닙니다. 이 두 벡터로는 원점을 지나는 한 직선상의 점들만 만들 수 있어서 전체 평면을 덮을 수 없습니다.
- u₁ = [2, 1]
- u₂ = [4, 2] (u₁의 2배)
기저는 유일하지 않고 여러가지 기저가 가능하지만 똑같은 차원에서는 기저 벡터의 개수는 항상 같습니다 (2차원에서는 항상 2개, 3차원에선 항상 3개). 기저가 바뀌면 같은 벡터라도 좌표 표현이 달라집니다
일차 독립(Linear Independence)
일차독립이란 벡터들의 집합에서 어떤 벡터도 다른 벡터들을 조합해서 만들 수 없다는 의미입니다.
일차독립인 경우를 살펴봅니다.
- 벡터 x = [1, 0] (오른쪽 방향)
- 벡터 y = [0, 1] (위쪽 방향)
이 두 벡터는 서로 완전히 다른 방향을 가리키므로, 벡터 x에 어떤 실수를 곱해도 y를 만들 수 없고, 벡터 y에 어떤 실수를 곱해도 x를 만들 수 었습니다. 따라서 일차독립입니다.
일차독립이 아닌 경우의 예입니다.
- 벡터 u = [2, 1]
- 벡터 v = [4, 2]
- 벡터 w = [6, 3]
여기서 v = 2×u이고, w = 3×u입니다. 즉, u 하나만 있으면 v와 w를 만들 수 있으므로 이들은 일차독립이 아닙니다.
일차독립인 벡터들은 각각이 고유한 방향성을 가지고 있어서, 어느 하나도 다른 것들로 대체할 수 없는 독립적인 존재라는 의미입니다.
일차 독립인 2개의 벡터를 화면에 그려줍니다.
행렬(Matrix)
행렬은 숫자들을 표 형태로 배열한 것입니다. 가로 방향으로 숫자들이 나열된 것을 행(row)이라 하고, 세로 방향으로 숫자들이 나열된 것을 열(column)이라 합니다.
다음은 2행 2열의 행렬입니다.
함수로서의 행렬
행렬을 함수처럼 생각할 수 있습니다.
파이썬 함수가 입력값을 받아서 처리한 후 결과값을 내놓는 것처럼, 행렬도 입력 벡터를 받아서 변환 과정을 거쳐 새로운 출력 벡터를 만들어냅니다.
이때 행렬이 하는 변환을 선형변환(linear transformation)이라고 부릅니다.
선형 변환(Linear Transformation)
선형변환은 벡터를 다른 벡터로 바꾸는 규칙입니다. 이때 벡터의 덧셈과 곱셈 성질이 그대로 유지됩니다.
행렬 A와 벡터 x가 있을 때, A × x = y 라는 계산을 통해 새로운 벡터 y를 만들어냅니다. 이 과정이 바로 선형변환입니다.
행렬의 종류에 따라 벡터 x를 다양하게 바꿀 수 있습니다:
- 회전 행렬: 벡터를 시계방향이나 반시계방향으로 돌림
- 확대/축소 행렬: 벡터를 크게 만들거나 작게 만들거나 늘림
- 반사 행렬: 벡터를 거울에 비친 것처럼 뒤집음
- 이동 행렬: 벡터의 위치를 다른 곳으로 옮김
정사각형에 변환 행렬(Transformation matrix)을 적용하여 평행사변형으로 바꾸는 코드입니다.
실행 결과입니다.
역행렬(Inverse Matrix)
역행렬은 원래 행렬과 곱했을 때 단위행렬이 나오는 특별한 행렬입니다.
A × A⁻¹ = I
여기서 A⁻¹는 A의 역행렬이고, I는 단위행렬(대각선이 모두 1이고 나머지는 0인 행렬)입니다
모든 행렬에 역행렬이 있는 것은 아닙니다. 역행렬이 존재하는 행렬을 가역행렬 또는 정칙행렬이라고 부릅니다.
실행 결과 역행렬을 출력해줍니다.
[[-2. 1. ]
[ 1.5 -0.5]]
특이행렬(Singular Matrix)
특이행렬은 역행렬이 존재하지 않는 정사각행렬입니다.
특이행렬의 특징은 다음과 같습니다.
- 행렬식(determinant)이 0입니다
- 계수(rank)가 행렬의 크기보다 작습니다
- 행이나 열 중에서 서로 의존적인 것들이 있습니다
다음 행렬에서 두 번째 행은 첫 번째 행을 1/2로 줄인 것과 같습니다. 이처럼 행들이 서로 독립적이지 않으면 특이행렬이 됩니다.
일반 숫자에서 0으로 나눌 수 없는 것처럼, 특이행렬도 나누기가 불가능합니다. 변환했을 때 일부 정보가 손실되어 원래대로 되돌릴 수 없기 때문입니다
연립방정식을 풀 때 해가 없거나 무수히 많은 해가 있는 경우에 특이행렬이 나타납니다.
np.linalg.inv 넘파이 함수를 사용하여 특이 행렬의 역행렬이 있는지 여부를 확인해봅니다.
실행결과 역행렬을 찾을 수 없다는 메시지가 출력됩니다.
Matrix is singular, cannot find its inverse.
단위 행렬(Identity matrix)
단위행렬은 대각선에는 1이 있고, 나머지 모든 자리에는 0이 있는 정사각행렬입니다.
단위행렬은 행렬의 곱셈에서 숫자 1과 같은 역할을 합니다.
- 일반 숫자: 5 × 1 = 5
- 행렬: A × I = A (어떤 행렬 A에 단위행렬 I를 곱해도 A 그대로)
단위 행렬이 중요한 이유
- 역행렬을 구할 때: A × A⁻¹ = I가 되는 것이 목표입니다
- 연립방정식 풀이에서 최종 답을 확인할 때 사용됩니다
- 행렬 변환에서 아무것도 하지 않는 기본 상태를 나타냅니다
단위 행렬을 생성하여 출력해봅니다.
실행결과 4 x 4 크기의 단위 행렬이 출력됩니다.
[[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]]
대각 행렬(Diagonal Matrix)
대각행렬은 주대각선(왼쪽 위에서 오른쪽 아래로 가는 대각선)에만 숫자가 있고, 나머지 자리는 모두 0인 정사각행렬입니다.
대각행렬은 다음과 같은 특징이 있습니다.
- 행렬식 계산이 쉬움: 대각선 원소들을 모두 곱하기만 하면 됩니다
3 × (-2) × 5 = -30
- 거듭제곱이 간단: 각 대각선 원소를 따로 거듭제곱하면 됩니다
- 역행렬 구하기 쉬움: 각 대각선 원소의 역수를 취하면 됩니다
복잡한 행렬을 대각 행렬로 바꿔서 고유값을 찾을때 사용됩니다.
대각 행렬을 생성하여 출력해봅니다.
실행결과 대각행렬이 출력됩니다.
[[1 0 0]
[0 2 0]
[0 0 3]]
직교 행렬(Orthogonal matrix)
직교행렬은 전치행렬과 역행렬이 같은 특별한 정사각행렬입니다.
아래 그림에서 보이듯이 2 x 2 크기의 단위 행렬은 전치 행렬과 역행렬이 똑같습니다.
수학적 정의: 행렬 A가 직교행렬이 되려면: AᵀA = AAᵀ = I 이고, 이는 Aᵀ = A⁻¹와 동치입니다.
AᵀA = I 라는 것은 A⁻¹A = I와 같은 의미입니다
따라서 Aᵀ = A⁻¹ (전치행렬 = 역행렬)
증명은 다음과 같습니다.
AᵀA = I 에서 양변에 A⁻¹을 오른쪽에서 곱하면
AᵀAA⁻¹ = IA⁻¹
AᵀI = A⁻¹ (∵ AA⁻¹ = I)
Aᵀ = A⁻¹
직교행렬의 핵심은 *전치행렬이 곧 역행렬이라는 점입니다. 이것이 직교행렬을 특별하게 만드는 가장 중요한 성질입니다.
역행렬을 구하기 어려운 일반 행렬과 달리, 직교행렬은 단순히 전치만 하면 역행렬을 얻을 수 있어서 계산이 매우 간단합니다.
기하학적 의미는 직교행렬의 행들과 열들은 모두 직교 단위벡터입니다.
두 벡터가 직교한다는 것은 서로 수직(90도)라는 것을 의미하며 직교하는 두 벡터의 내적은 0입니다.
다음 행렬도 직교행렬인데 회전 행렬(rotation matrix)이라고 부르며 다음과 같은 성질이 있습니다.
회전 행렬의 물리적 특성은 다음과 같습니다.
- 거리와 각도를 보존합니다 (등거리 변환)
- 벡터의 크기를 변화시키지 않습니다
- 도형의 모양과 크기를 그대로 유지하면서 회전만 시킵니다
행렬 곱셈(Matrix multiplication)
행렬 곱셈은 두 행렬을 특별한 방법으로 곱해서 새로운 행렬을 만드는 연산입니다.
두 행렬 A × B를 곱하려면 첫 번째 행렬 A의 열 개수와 두 번째 행렬 B의 행 개수가 같아야 합니다. 결과 행렬의 크기는 [A의 행 개수 × B의 열 개수]가 됩니다.
[2 × 3] × [3 × 2] = [2 × 2] ✅ 행렬 곱셈 가능 (3 = 3)
[3 × 2] × [2 × 3] = [3 × 3] ✅ 행렬 곱셈 가능 (2 = 2)
[3 × 2] × [3 × 2] = ? ❌ 행렬 곱셈 불가능 (2 ≠ 3)
행렬 곱셈을 계산하기 위해 결과 행렬의 각 원소는 행과 열의 내적으로 구합니다.
계산 과정:
- (1,1) 위치: (1×3) + (2×1) = 5
- (1,2) 위치: (1×2) + (2×2) = 6
행렬 곱셈에서 주목할 만한 성질입니다.
- 교환법칙이 성립하지 않음: A×B ≠ B×A (일반적으로)
- 결합법칙은 성립: (A×B)×C = A×(B×C)
- 분배법칙 성립: A×(B+C) = A×B + A×C
행렬 곱셈의 교환법칙이 성립되지 않는 것은 행렬 변환의 순서가 중요하다는 것을 의미합니다. B를 먼저 적용하고 A를 나중에 적용한 것과 A를 먼저 적용하고 B를 나중에 적용하는 것과 항상 같지 않습니다.
다음 예제에선 행렬 변환 순서가 바뀌어도 똑같은 결과를 보여줍니다.
실행결과입니다.
대각합(Trace)
대각합은 행렬의 주대각선에 있는 모든 원소들을 더한 값입니다.
행렬 A의 대각합을 구해봅니다.
tr(A) = 3 + (-2) + 6 = 7
대각합의 중요한 성질은 다음과 같습니다.
1. 기저 변환에 불변
- 같은 선형변환을 다른 좌표계로 표현해도 대각합은 동일합니다
- 즉, 행렬의 "본질적인" 성질을 나타냅니다
2. 고유값의 합
- tr(A) = λ₁ + λ₂ + ⋯ + λₙ (모든 고유값의 합)
- 고유값을 직접 구하지 않고도 그 합을 알 수 있습니다
3. 선형성
- tr(A + B) = tr(A) + tr(B)
- tr(cA) = c × tr(A)
대각합은 정사각행렬에만 정의됩니다. 직사각행렬에서는 대각합을 구할 수 없습니다.
행렬식(Determinant)
행렬식은 행렬이 공간을 얼마나 확대하거나 축소시키는지를 나타내는 값입니다.
단위 면적(또는 부피)이 1인 영역이 행렬 변환을 거쳐서 얼마나 커지거나 작아지는지를 측정합니다.
계산 방법
행렬 A의 행렬식을 구해봅니다.
det(A) = (3×2) - (1×0) = 6
이는 단위 정사각형(면적=1)이 이 행렬로 변환되면 면적이 6배가 된다는 뜻입니다.
실행결과 행렬식 계산 결과가 출력됩니다.
Determinant of A: -2.0
행렬식의 의미는 다음과 같습니다.
- 양수 (+) : 면적/부피 확대, 방향 유지
- 음수 (-) : 면적/부피 확대 + 방향 뒤바뀜 (거울상)
- 0 : 차원이 줄어듦 (면적→선, 부피→면) 1 : 크기와 방향 모두 유지 (강체 변환)
중요한 성질들
- det(AB) = det(A) × det(B)
- det(A⁻¹) = 1/det(A)
- det(Aᵀ) = det(A)
- 역행렬이 존재 ⟺ det(A) ≠ 0
직관적 이해
- det = 2: "모든 것이 2배로 커짐"
- det = 0.5: "모든 것이 절반으로 작아짐"
- det = -1: "거울에 비친 것처럼 뒤집어짐"
- det = 0: "3차원이 2차원으로 눌려짐"
계수(Rank)
행렬의 계수는 행렬에서 서로 독립적인 벡터의 최대 개수를 의미합니다. 쉽게 말해, 행렬의 행들이나 열들 중에서 진짜로 다른 방향을 가리키는 벡터가 몇 개나 되는지를 나타내는 수치입니다.
계수는 선형변환이 공간을 어떻게 변화시키는지 알려줍니다:
다시 말해 계수는 선형변환이 얼마나 많은 차원을 보존하는지 알려주는 숫자입니다.
예를 들어보겠습니다.
2×2 행렬은 2차원 평면입니다.
계수가 2라면 2차원을 유지하지만 계수가 1이라면 직선으로 압축되고 계수가 0이라면 점으로 압축됩니다. 계수가 낮아질 수록 정보가 손실됩니다.
3×3 행렬은 3차원 공간입니다.
계수가 3이라면 3차원을 그대로 유지하고 계수가 2이면 평면으로 압축되고 계수가 1이면 직선으로 압축됩니다. 계수가 낮아질 수록 정보가 손실됩니다.
즉, 계수가 클수록 더 많은 차원 정보를 보존하게 됩니다.
행렬의 계수를 계산하는 코드입니다.
[[1 2]
[1 2]]
Rank: 1
[[1 2]
[3 4]]
Rank: 2
[[1 0 2]
[0 1 3]
[1 1 5]]
Rank: 2
고유벡터(Eigenvectors)와 고유값(Eigenvalues)
고유 벡터는 선형 변환 후에도 방향이 바뀌지 않는 벡터입니다. 방향은 변하지 않지만 크기는 변할 수 있습니다. 이 크기를 고유값이라고 합니다. 고유값은 고유벡터가 얼마나 늘어나거나 줄어드는지를 나타내는 수치입니다:
- 고유값이 1보다 크면 고유벡터가 늘어납니다.
- 고유값이 1이면 벡터 크기가 그대로 유지됩니다.
- 고유값이 0과 1사이 값이면 벡터 크기가 줄어듭니다.
- 고유값이 0이면 고유 벡터가 영벡터가 됩니다.
- 고유값이 음수이면 벡터의 방향이 반대가 되며 벡터 크기는 고유값만큼 변합니다.
Av = λv (행렬 × 고유벡터 = 고유값 × 고유벡터)
행렬 A(선형 변환)를 벡터 v(고유벡터)에 곱한 결과가, 그 벡터 v에 상수 λ(고유값)를 곱한 것과 같다는 뜻입니다. 즉, 선형변환 후에도 벡터의 방향은 그대로 유지되고 크기만 λ배 변한다는 의미입니다.
실행 결과입니다. 행렬 A와 함께 고유값, 고유벡터를 출력합니다.
Matrix A:
[[1 2]
[2 3]]
Eigenvalues: [-0.23606798 4.23606798]
Eigenvectors:
[[-0.85065081 -0.52573111]
[ 0.52573111 -0.85065081]]
실행 결과에는 3개의 그래프가 세로방향으로 나란히 배치되는데 각각에 대한 설명을 추가해봅니다.
행렬 A(선형변환)에 의해서 회색 단위원이 초록색 타원으로 변환됩니다.
빨간 화살표와 파란 화살표는 고유벡터입니다.
이 화살표들은(고유벡터) 원이 변형된 후에도 방향을 유지합니다.
행렬 A에 의해 변환되기 전의 상태를 보여줍니다.
모든 화살표의 길이는 1로 표준화 되어있습니다. 고유벡터 방향의 변화를 살펴보기 위해서입니다.
연한 빨강, 연한 파랑 화살표는 원래 고유벡터 방향입니다.
모든 화살표 길이가 1로 동일합니다.
회색원은 행렬 A에 의한 변화를 시각화해서 보여주기 위해 그려놓은 것입니다.
행렬 A에 의해서 선형 변환후의 결과를 보여줍니다.
빨간 화살표는 방향이 180도 뒤바뀌고 크기가 변화되었습니다. (λ₁ = 음수)
파란 화살표는 원래 방향은 유지하고 크기가 변화했습니다. (λ₂ = 양수)
화살표 길이는 고유값의 크기입니다.
고유값 1: -0.236 (음수) → 방향 반전 + 크기 0.24배
고유값 2: 4.236 (양수) → 방향 유지 + 크기 4.24배
참고
Linear Algebra Concepts Every Data Scientist Should Know
Comments ()